Conceptos Previos

Para aprender a derivar es necesario conocer los siguientes conceptos:

• Radio: Línea que va del centro de la circunferencia a uno de sus extremos.
• Diámetro: Línea que pasa por la mitad de la circunferencia, de un extremo a otro.
• Secante: Línea que divide la circunferencia en dos.
• Tangente: Línea que toca un solo punto de la circunferencia pero no la atraviesa. 

Pasos para Derivar por Límites

Para empezar, comenzaremos con un ejercicio sencillo:

                       1. f(x)= x^2 + 4x − 5

1. Lo primero que hay que hacer es tener en cuenta la siguiente ecuación:

              

                  f'(x)= lim     f(x+h)-f(x)

                          h-0           h

2. Seguido de esto hay que reemplazar la ecuación: la x se reemplaza por (x+h) y -f(x) se reemplaza por toda la función. Así

                 f'(x)= lim   (x+h)^2 -x^2  +  4(x+h) - 4x

                          h-0           h                     h

El 5 no se coloca por que la derivada de cualquier número es siempre igual a 0.

3. Ahora, se operan la funciones; las funciones que están elevadas a cualquier número necesitan ser operadas por medio del triangulo de pascal; en este caso como (x+h) esta elevada a la 2 quedaría:

(x^2+2xh+h^2) porque:                 

                                       

1er término al cuadrado + 2 veces el 1er término por el 2do + el último término al cuadrado.

                 f'(x)= lim  x^2+2xh+h^2-x^2   +  4x+4h - 4x

                          h-0             h                         h

4. Eliminamos términos semejantes.

                 f'(x)= lim 2xh+h^2  +  4h

                          h-0       h           h

5. Una vez tengamos los términos finales es hora de hallar el factor común, el cual es la h (siempre es la h) para poder así cancelarla con la h del denominador.

                f'(x)= lim h(2x+h^2)  + h(4)

                         h-0        h           h

5. Una vez se hayan eliminado las aches, ahora si podemos despejar el limite. 

                f'(x)=2x+0^2  + 4

                               

6.  Finalmente la función ha sido derivada, así que ya no es necesario colocar el limite (durante toda la derivación es necesario colocar el limite)

               f'(x)= 2x+ 4

Veamos ahora unos Ejemplos

1. f(x)= 3x^2 + 2x -10

    f'(x)= lim    3(x+h)^2-3x^2   +  2(x+h)-2x

             h-0              h                      h

   

    f'(x)= lim   3(x^2+2xh+h^2)-3x^2  + 2x+2h-2x

             h-0                    h                     h

    f'(x)= lim  3x^2+6xh+3h^2-3x^2  +  2h

             h-0               h                       h

    f'(x)= lim  6xh+3h^2  +  2h

             h-0       h              h

    f'(x)= lim  h(6x)  +  h(2)

             h-0     h          h

    f'(x)= 6x+2

2. f(x)= x^7 

f'(x)= lim  (x+h)^7-x^7

         h-0          h

f'(x)= lim

        h -0 x^7+7x^6h+21x^5h^2+35x^4h^3+35x^3h^4+21x^2h^5+7xh^6+h^7 - x^7

                                                    h

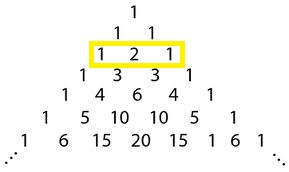
-> Es importante tener en cuenta que ha medida que se va operando (usando el triangulo de pascal) las x van disminuyendo y la h aumentando

f'(x)= lim    h(7x^6+21x^5h+35x^4h^2+35x^3h^3+21x^2h^4+7xh^5+h^6)

         h-0                                            h

f'(x)= 7x^6 

3. f(x)=   8     + x^3   

            x^2

                           8              -    8  

 f'(x)=lim    x^2+2xh+h^2        x^2       +   x^3+3x^2h+3xh^2+h^3 - x^3

         h-0                       h                                         h

Ahora multiplicamos numerador 1 con denominador 2 y denominador 2 con numerador 1 (esto irá en el numerador) luego denominador 1 con denominador 2 (esto va en el denominador) .... Sin olvidar todo esto va sobre h.

              8x^2 - 8x^2+16xh+8h^2

f'(x)= lim     x^4+2x^3h+x^2h^2      +    3x^2h+3xh^2+h^3

         h-0                  h                                       h

Ahora bien, para operar la primera función utilizamos la conocida "ley de oreja" (los términos externos se multiplican entre si quedando en el numerador, los internos se multiplican entre si quedando en el numerador); como la h no tienen el denominador señalado, esto significa que este es 1.

f'(x)= lim           1(16xh+8h^2)          +  3x^2h+3xh^2+h^3

         h-0  h(x^4+2x^3h+x^2h^2)                      h

f'(x)= lim           h(16x+8h)               +   h(3x^2+3xh+h^2)

         h-0  h(x^4+2x^3h+x^2h^2)                      h

f'(x)= 16x    +  3x^2

         x^4

f'(x)=  16    +  3x^2

         x^3

4. f(x)= x^3 - 3x^2 + 4

                  x^2

Para poder simplificar el valor de las x, podemos separar el fraccionario de la siguiente manera

f(x)= x^3 - 3x^2 +4   entonces  f(x)= x - 3 + 4 

        x^2    x^2

Después de realizar este paso podemos darnos cuenta que la función que ahora tenemos es:

f(x) = x+1

f'(x)= lim  (x+h)+1 - (x+1)

         h-0        h

f'(x)= lim  x+h+1-x-1

         h-0      h

f'(x) = lim   h

         h-0   h

f'(x)=1

5.  f(x)= x-3x^-2

                         

f'(x)= lim  (x+h)- 3(x+h)^-2 - (x-3x^-2)    

        h-0                   h

cuando se tiene un exponente negativo como el x^-2 se cambia de numerador a denominador, cambiando su signo, debido a que un exponente no puede ser negativo y nos queda 

  1   

x^2 

              

               x+h -     3      - x -  3  

f'(x)= lim          (x+h)^2        x^2

        h-0                  h

                    hx^2(x^2+2xh+h^2) -3x^2 - 3(x^2+2xh+h^2)

f'(x)= lim                        x^2(x^2+2xh+h^2)                           

         h-0                                h

f'(x)= lim    hx^4 + 2x^3h^2 + x^2h^4+ 3x^2 - 3x^2-6xh-3h^2

         h-0                       h(x^4+2x^3h+x^2h^2)

f'(x)=lim    h ( x^4 + 2x3h+ x^2h^3 - 6x - 3h)   

        h-0              h(x^4+2x^3h+x^2h^2)

f'(x)= x^4- 6x

            x^4

f'(x)=  1 - 6x^-3

Ejercicios

Realiza los siguientes ejercicios para reforzar lo que has aprendido:


1. f(x)= x^3-6
             x^2


2. f(x)=    5        +   x(x^2+1)
            (2x)^3


3. f(x)= 3x(6x-5x^2)+   4    - 3x^-2
                                x^3


4. f(x)= x^4/5-x^2/3




5. f(x)=      2     
            x^1/3 +5